|
W niniejszym opracowaniu przedstawiono sposób szacowania cyklu życia urządzeń infrastruktury teleinformatycznej według metody opracowanej przez Karla Whelana. Metodę tą Karl Whelan pokazał w swojej pracy w 2000 roku („Computers, Obsolescence, and Productivity” – Karl Whelan, Division of Research and Statistics, Federal Reserve Board, February, 2000) w trakcie badań nad wpływem komputeryzacji na wzrost wydajności pracy w gospodarce Stanów Zjednoczonych stosując metodykę NIPA (the U.S. National Income and Product Accounts).
Karl Whelan w trakcie swoich badań przyjął następujący podział elementów infrastruktury teleinformatycznej (według standardów NIPA):
- komputery klasy mainframe (centralne komputery klasy mainframe, wraz z systemem operacyjnym, obsługujące komputery wielu użytkowników);
- komputery osobiste (wysokiej klasy komputery stacjonarne, wraz z systemem operacyjnym, do użytku osobistego, domowego i biurowego);
- terminale (urządzenia pozwalające na pracę z komputerem, bądź systemami komputerowymi);
- urządzenia pamięci masowej (dyski twarde, macierze dyskowe);.
- drukarki (urządzenia współpracujące z komputerem, służące do drukowania tekstu i obrazu.
Powyższy podział urządzeń z klasy wyposażenia komputerowego, wraz z odpowiadającymi im ekonomicznymi stopami amortyzacji (ang. depreciation rates), publikowany jest okresowo przez NIPA i uwzględniany w księgowości przedsiębiorstw gospodarki Stanów Zjednoczonych.
W swoim opracowaniu Karl Whelan wykorzystał model Solow’a (Solow Vintage Model) i porównał z wynikami badań Olivera zauważając pewne anomalie. Następnie rozszerzył model Solow’a o czynnik związany z technologicznym zużyciem (ang. technological obsolescence) poszczególnych elementów infrastruktury teleinformatycznej uzyskując wyniki o wiele bardziej zbliżone do rzeczywistości i różniące się od publikowanych wcześniej danych przez NIPA. Różnice między danymi uzasadnił technologicznym zużyciem komputerów, jednocześnie uzasadniając tym zauważone u Olinera anomalie. Zjawisko zużycia technologicznego dla wyposażenia komputerowego objawia się poprzez wcześniejsze wycofanie z użytkowania danego urządzenia nie z powodu utraty produktywności (Solow Vintage Model), a z powodu zbytniego oddalenia od najnowszych technologii teleinformatycznych aktualnych na dzień wycofania danego urządzenia z eksploatacji (ang. vintage).
W celu przybliżenia metody opracowanej przez Karla Whelana w dalszej części niniejszego opracowania pokazano mechanizm wyznaczania ekonomicznej amortyzacji (ang. economic depreciation) na przykładzie komputera osobistego. Następnie przedstawiono wzór na wyznaczenie wieku wycofania urządzenia z eksploatacji, omawiając wpływ poszczególnych czynników na wiek złomowania urządzenia, po czym porównano wyniki uzyskane na cykl życia dla różnych klas elementów infrastruktury teleinformatycznej. Na koniec zaś przedstawiono wnioski związane z wpływem wyznaczania wieku wycofania urządzenia z eksploatacji w poszczególnych sektorach gospodarki narodowej.
Podstawowym elementem dzisiejszych systemów informatycznych jest komputer klasy PC. Dlatego też poniżej pokazano sposób określania cyklu życia takiego komputera. Analogicznie można oszacować cykl życia pozostałych składników wyposażenia systemów informatycznych.
Wartość komputera, który właśnie wprowadzono do użytku, spada wraz z czasem jego eksploatacji. Wartość komputera związana jest ściśle z jego krańcową produktywnością (ang. marginal productivity).
Produktywność oznacza relację efektów ekonomicznych osiągniętych dzięki wprowadzeniu danego elementu infrastruktury teleinformatycznej do sumy nakładów ekonomicznych wydatkowanych na wprowadzenie danego urządzenia do eksploatacji.
W przypadku komputera PC nakładami ekonomicznymi mogą być koszty serwisu (poziom utrzymania), natomiast efektami ekonomicznymi zyski osiągane dzięki wprowadzeniu i użytkowaniu komputera PC.
Krańcowa produktywność kapitału jest to przyrost produkcji na skutek wzrostu nakładów kapitału o jednostkę. Gdy krańcowa produktywność komputera spadnie poniżej kosztów jego serwisu, wtedy utrzymywanie danego komputera osobistego jest nieopłacalne i zazwyczaj takie urządzenie jest złomowane.
Krańcowa produktywność urządzenia zmienia się w trakcie jego używania w zależności od następujących współczynników:
- współczynnik r związany ze stopą procentową obligacji rocznych skarbu państwa (uwzględnienie procesów inflacyjnych),
- współczynnik γ – g związany ze spadkiem cen komputerów będących na podobnym poziomie rozwoju technologii informatycznych (każdy poziom rozwoju komputerów w danym okresie czasu charakteryzuje się pewnymi parametrami jego wyposażenia – procesor, płyta główna, pamięć RAM, dysk twardy – stanowiąc linię produktów będących na podobnym poziomie rozwoju technologii informatycznych) oraz związany z bezpośrednim spadkiem wartości komputera w wyniku rozpoczęcia jego eksploatacji (zaraz po „rozpakowaniu” komputera traci on automatycznie na wartości),
- współczynnik δ związany z zużyciem fizycznym komputerów, gdy komputer jest używany przez użytkownika.
Jednocześnie należy zauważyć, że eksploatacja komputera wymaga odpowiedniego poziomu jego utrzymania. Poziom utrzymania komputera opisuje współczynnik s, który jest współczynnikiem kosztu jego serwisu.
Wyznaczenie amortyzacji komputera
W latach 1989-1994 Oliner wyprowadził wzory na amortyzację dla czterech kategorii wyposażenia komputerowego: komputery klasy mainframe, dyski twarde, drukarki, terminale. Rysunek 1. pokazuje przybliżony rozkład amortyzacji (ang. quality-adjusted depreciation schedule) uzyskany w trakcie tych badań, których wyniki Departament Handlu BEA zastosował do publikowania księgowych wartości odtworzenia danej klasy urządzeń (ang. wealth stocks).
Rysunek 1. Rozkłady amortyzacji dla wyposażenia komputerowego.
Rysunek 2. pokazuje odpowiadające stopy amortyzacji (ang. depreciation rates). Przybliżone ekonomiczne stopy amortyzacji (ang. economic depreciation rates) zmniejszają się w czasie, gdyż BEA stosowała różne dane dla rozkładów inwestycyjnych (ang. schedule to investment) z różnych okresów rozwoju technologii informatycznych (ang. vintage).
Rysunek 2. Stopy amortyzacji dla wyposażenia komputerowego.
Jeśli model Solow’a jest prawidłowy, to te oszacowane ekonomiczne rozkłady amortyzacji (ang. economic depreciation schedules) powinne odpowiadać rozkładowi dla fizycznego zużycia. Przedstawione oszacowania nie wyglądają na rozkłady odpowiadające fizycznemu zużyciu urządzeń komputerowych. Istnieją trzy anomalie, które wydają się niespójne z interpretacją jedynie fizycznego zużycia komputerów. Po pierwsze rozkłady te nie są krzywymi geometrycznymi, przy czym stopa amortyzacji (ang. depreciation rates) zmniejsza się wraz ze wzrostem wieku urządzeń (za wyjątkiem drukarek). Stoi to w sprzeczności z rozkładami dla innych środków trwałych, dla których geometryczna amortyzacja jest przydatnym przybliżeniem. Po drugie nachylenie krzywej w dół w funkcji czasu, w tych rozkładach wydaje się niespójne w porównaniu z interpretacją fizycznego zużycia tych urządzeń. Raczej nie należy się spodziewać, że wyposażenie komputerowe staje się bardziej niezawodne wraz z upływem czasu. Dzieje się wręcz odwrotnie.
Po trzecie, co ważniejsze, wartości te wydają się być po prostu zbyt wysokie jak na współczynniki fizycznego zużycia. Tablica 1. pokazuje stopy amortyzacji według NIPA z 1997 roku dla wszystkich kategorii wyposażenia. Godne uwagi jest to, że oszacowane stopy amortyzacji oparte na badaniach Olinera są wyższe niż stopy amortyzacji dla wszystkich innych kategorii urządzeń za wyjątkiem samochodów. Jeszcze bardziej godne uwagi jest to, że dla wszystkich typów urządzeń stopy amortyzacji NIPA nie są oparte na oszacowanym przybliżeniu i skutkiem tego są połączeniem efektów zarówno fizycznego zużycia jak i odbiciem zmian technologicznych. Swobodne obserwacje sugerują, że jest to wysoce niepodobne by współczynniki fizycznego zużycia dla komputerów były o wiele wyższe niż dla innych typów urządzeń. Dodatkową zagadką jest fakt, że Oliner prowadził badania w oparciu o sprzęt wyprodukowany przez IBM, który to sprzęt w tamtym czasie był sprzedawany łącznie z pakietem usług serwisowych: IBM gwarantował naprawić, bądź wymienić wadliwe wyposażenie. Z tego też względu wyposażenie, badane przez Olinera, powinno mieć oszacowane współczynniki fizycznego zużycia równe zeru ze względu na to, że IBM przejmował na siebie koszt fizycznego zużycia urządzeń. Badania Olinera z 1994 roku urządzeń komputerowych również nie podają poprawnie fizycznego zużycia i dodatkowo przedstawiają kapitał obrotowy (ang. productive stock) oparty na przyjęciu współczynnika fizycznego zużycia równego zeru.
Wszystkie te argumenty sugerują, że dane te nie były wygenerowane zgodnie z modelem Solow’a.
Dalej zostanie przedstawione rozszerzenie modelu Solow’a, dzięki któremu to modelowi wyjaśnione zostaną wszystkie trzy anomalie związane ze wzorami Olinera:
- niegeometryczna krzywa;
- odchylenie krzywej w dół w czasie;
- przybliżone ekonomiczne stopy amortyzacji są większe aniżeli współczynniki fizycznego zużycia.
Tabela 1. Stopy amortyzacji dla urządzeń według NIPA z 1997 roku.
|
Computing Equipment:
|
|
Electrical Transmission
|
0.05
|
|
Mainframes
|
0.30
|
Cars
|
0.28
|
|
Terminals
|
0.27
|
Trucks, Buses, and Trailers
|
0.18
|
|
Storage Devices
|
0.28
|
Aircraft
|
0.08
|
|
Printers
|
0.35
|
Ships and Boats
|
0.06
|
|
Personal Computers
|
0.11
|
Railroad Equipment
|
0.06
|
|
Other Office Equipment
|
0.31
|
Household Furniture
|
0.14
|
|
Communications Equipment
|
0.11
|
Other Furniture
|
0.12
|
|
Instruments
|
0.14
|
Farm Tractors
|
0.15
|
|
Photocopying Equipment
|
0.18
|
Construction Tractors
|
0.16
|
|
Fabricated Metals
|
0.09
|
Agricultural Machinery
|
0.12
|
|
Steam Engines and Turbines
|
0.05
|
Construction Machinery
|
0.16
|
|
Internal Combustion Engines
|
0.21
|
Mining and Oilfield Machinery
|
0.15
|
|
Metalworking Machinery
|
0.12
|
Service Industry Machinery
|
0.15
|
|
Special Industrial Machinery
|
0.10
|
Other Electrical Equipment
|
0.18
|
|
General Industrial Machinery
|
0.11
|
Miscellaneous Equipment
|
0.15
|
Anomalie pokazane w Tabela 1., które są stopą amortyzacji NIPA dla komputerów osobistych, powstały na skutek przybliżenia przez BEA rozkładu dla komputerów klasy mainframe oszacowanego przez Olinera w 1989 roku, który to rozkład nie dopuszczał zmian amortyzacji w czasie. Przybliżenie to dokonano ze względu na fakt, że badania Olinera nie uwzględniły komputerów osobistych. Dlatego też rozkłady dla każdej innej kategorii wyposażenia komputerowego zmniejszają się w czasie, przy czym komputery osobiste okazują się kategorią urządzeń najwolniej tracącą na wartości. BEA przyznała, że jest to anomalia i postanowiła wprowadzić nowy kapitał akcyjny (ang. capital stock) pozwalający oszacować dla komputerów osobistych odpowiadające stopy amortyzacji bliższe tych, które były używane dla innych klas wyposażenia komputerowego.
Obliczenie kosztu serwisu i wieku wycofania z eksploatacji
Rozszerzenie modelu Solowa (Obsolescence Model) spowodowane zostało na skutek dwóch obserwacji. Pierwszą z nich jest fakt, że podstawowy model jest niespójny z technologicznym zużyciem (ang. technological obsolescence). Model Solow’a przewiduje, że firmy nigdy nie wycofają z eksploatacji urządzenia, które jest produktywne, mimo, że jest przestarzałe. Model ten właściwie sugeruje jako optymalną strategię, by po prostu pozwolić na eksploatację urządzenia aż do jego stopniowej degradacji. Druga obserwacja jest taka, że systemy komputerowe są zazwyczaj złożone i mogą być użytkowane jedynie przy zapewnieniu technicznego wsparcia oraz utrzymania. W ostatnich kilkunastu latach zaobserwowano gwałtowne zapotrzebowanie na takich pracowników jak administratorzy sieci komputerowych. Pokazuje to jak duże muszą być wydatki na wsparcie i utrzymanie infrastruktury teleinformatycznej przy inwestycjach w technologie IT. Jednocześnie badania Gartner Group w 1999 roku (prywatnej firmy konsultingowej) pokazują, że w 1998 roku na każdego dolara wydanego przez firmy na sprzęt komputerowy, następne 2,3 dolara firmy wydawały na pracowników i konsultantów IT. Model technologicznego zużycia wykorzystuje fakt istnienia kosztów serwisu w celu uzasadnienia zjawiska technologicznego zużycia wyposażenia komputerowego. Jeżeli krańcowa produktywność urządzenia spadnie chociaż raz poniżej kosztów serwisu, wtedy firma wycofa z eksploatacji dane urządzenie.
Teoria
Poniżej sformułowano pojęcie kosztów serwisu:
dla każdego komputera zakupionego w danej linii technologicznego rozwoju υ, firmy muszą ponieść koszt utrzymania dla każdego okresu równego części s oryginalnej ceny zakupu, pυ(υ).
Z tego też względu jeśli firma zakupiła komputer za 1000 dolarów i s = 0.15, to firma musi zapłacić 150 dolarów rocznie na serwis tego urządzenia. Funkcja dochodu firmy może być wyrażona jak poniżej:
πυ(t) = A(t)Lυ(t)α(t)Kυ(t)β(t) (I(υ)eγυe-δ(t-υ))1-α(t)-β(t)
–rυ(t)I(υ)e-δ(t-υ) - rο(t)Kυ(t) - ω(t)Lυ(t) – spυ(υ)I(υ)e-δ(t-υ) (1)
Należy zauważyć, że koszt serwisu nie ma bezpośredniego efektu na krańcową produktywność innych składników, które mają znaczenie w modelu Solow’a. Z tego też względu pierwszy rząd składników, które odpowiadają za pracujący i stały kapitał bez względu na linię technologicznego rozwoju (ang. vintage), nie ulegają zmianie, oprócz jednego ważnego składnika. Jak poprzednio pokazano użytkowanie komputera powoduje, że krańcowa produktywność jednostki kapitału komputera zmniejsza się w czasie przy współczynniku γ-g. Teraz zaś zamiast pozwolić by krańcowa produktywność zmniejszała się wraz ze stopniową degradacją do zera, występuje zjawisko polegające na tym, że gdy komputer osiągnie wiek T, w którym nie można pokryć kosztów utrzymania, wtedy jest uważany za zużyty i jest złomowany. Wzór na agregację kapitału komputera (ang. aggregate komputer capital stock) przybierze wtedy postać:
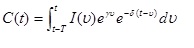 (2) (2)
Rysunek 3. Wiek wycofania z eksploatacji a krańcowa produktywność komputera PC
Rysunek 3. pozwala uchwycić skutki powyższego wzoru na ekonomiczną amortyzację. Na rysunku przedstawiono krzywą w czasie dla krańcowej produktywności urządzenia z danej linii rozwoju technologicznego dla ustalonej listy wartości r, δ oraz γ-g, a także dla dwóch wartości kosztu serwisu: s=0, w przypadku modelu zredukowanego do modelu Solow’a: s=0.07. Ponieważ firmy muszą obecnie płacić koszty serwisu, by użytkować komputer, więc równość pomiędzy stawką opłaty (ang. rental rate) a krańcową produktywnością środków kapitałowych (ang. capital needs) jest przedstawiona jak poniżej:
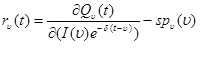 (3) (3)
Przy zakupie komputera o znacznej wartości, aktualna potrącona wartość tych opłat musi wciąż być równa cenie zakupu:
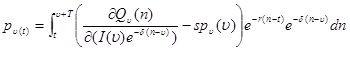 (4) (4)
Tak więc, dla danej ceny nabycia, krańcowa produktywność jednostki kapitału komputera musi być wyższa, gdy jest uwzględniany koszt serwisu.
Teraz należy wziąć pod uwagę krzywą ceny komputera w funkcji jego wieku. Na Rysunek 3. cena ta jest wyznaczona przez powierzchnię ograniczoną powyżej kosztu serwisu i poniżej krzywej krańcowej produktywności. Co ważniejsze, wraz z wiekiem urządzenia, powierzchnia ta zmniejsza się o wiele szybciej aniżeli krańcowa produktywność komputera, osiągając wartość zero przy wieku wycofania z eksploatacji. Od tego momentu ta krańcowa produktywność zmniejsza się zgodnie ze współczynnikiem g-γ w czasie, co spowodowane jest tym, że cena komputera spada w funkcji czasu szybciej aniżeli g-γ-δ, więc ekonomiczna stopa amortyzacji dla komputerów jest większa niż δ+γ.
Wiek wycofania z eksploatacji jest wyprowadzony jako rozwiązanie równania nieliniowego:
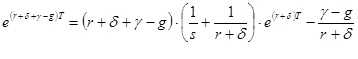 (5) (5)
Podczas gdy rozwiązanie tego wyrażenia wymaga stosowania metod numerycznych, można pokazać, że posiada on tez i intuicyjne właściwości takie, że im szybszy jest współczynnik przybliżonego spadku ceny dla nowych komputerów γ-g i wyższy koszt serwisu, to krótszy jest czas wycofania z eksploatacji. Definiując τ=t-υ dostajemy ekonomiczny rozkład amortyzacji:
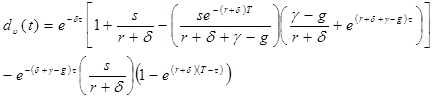 (6) (6)
To rozszerzenie modelu Solow’a (które nazywa się The Obsolescence Model) może wyjaśnić wszystkie trzy anomalie przytoczone na początku rozważań . Niegeometryczna ekonomiczna amortyzacja pokazana formalnie w powyższym równaniu jest intuicyjną cechą modelu jak pokazano na Rysunek 3. Odchylenie krzywej w dół w rozkładach przybliżonej ekonomicznej amortyzacji jest porównywane do zwiększania tempa technologicznego postępu, przy czym krzywa ta wydaje się pasować do przyśpieszenia zmian technologicznych w przemyśle komputerowym z początku lat osiemdziesiątych. Ostatecznie, co najważniejsze, model ten wyjaśnia dlaczego przybliżona ekonomiczna stopa amortyzacji, użyta do konstruowania rzeczywistej wartości odtworzenia komputera (ang. wealth stock) przez NIPA, jest taka wysoka. Nawet jeśli współczynnik fizycznego zużycia byłby równy zeru, przewidywany wcześniejszy czas wycofania z eksploatacji może oznaczać, że komputery wciąż tracą swoją wartość z upływem lat o wiele szybciej, aniżeli wynikałoby to z fizycznego ich zużycia.
Wpływ poszczególnych parametrów na wiek wycofania z eksploatacji
Czas ekonomicznego zużycia komputera T określa się jako czas, przy którym krańcowa produktywność spada poniżej kosztu serwisu tego komputera. Po tym czasie większość firm wycofuje dany komputer z eksploatacji zastępując go nowym (w rozumieniu nowego produktu z aktualnej linii rozwoju technologii informatycznych).
Czas wycofania komputera z eksploatacji pokazano w wyrażeniu (5). Równanie to można rozwiązać jedynie z zastosowaniem metod numerycznych (Rysunek 4).
Przykładowo: przyjmując stosowne wartości dla poszczególnych współczynników: γ-g = 0,33 (spadek wartości komputerów w skali roku – 33%), r = 0,1 (stopa oprocentowania obligacji rocznych skarbu państwa – 10%), δ = 0,05 (fizyczne zużycie komputera w skali roku – 5%) oraz s = 0,25 (koszt serwisu na poziomie 25% rocznie) otrzymujemy czas wycofania komputera z eksploatacji w granicach 4 lat. Należy przy tym zauważyć, że czas wycofania z eksploatacji komputera bardzo mocno zależy zarówno od kosztu serwisu, jak i spadku cen komputerów w skali roku.
Rysunek 4. Wpływ inflacji na wiek wycofania z eksploatacji komputera PC
Z powyższego rysunku wynika, że czynnik inflacyjny ma niewielkie znaczenie przy ustalaniu wieku złomowania komputera PC. Przy czym można zauważyć, że im mniejsza inflacja tym wiek złomowania nieznacznie spada.
Rysunek 5. Wpływ fizycznego zużycia na wiek wycofania z eksploatacji komputera PC
Obecnie fizyczne zużycie komputerów jest praktycznie bliskie zeru. Stąd dla komputerów osobistych wpływ fizycznego zużycia na wiek złomowania będzie niewielki, natomiast dla innych rodzajów wyposażenia (np. drukarki) będzie poważny.
Rysunek 6. Wpływ kosztu serwisu na wiek wycofania z eksploatacji komputera PC
Z powyższego rysunku wynika, że im wyższy koszt serwisu komputera tym krótszy jest jego czas eksploatacji, przy czym należy wziąć pod uwagę, że koszty serwisu nie dotyczą np. wymiany płyty głównej, wymiany procesora itp.
Rysunek 7. Wpływ szybkości spadku cen na wiek wycofania z eksploatacji komputera PC
Wpływ szybkości spadku cen komputerów jest bardzo ściśle związany z wprowadzaniem na rynek produktów z następnych wyższych poziomów rozwoju technologii informatycznych, stąd współczynnik spadku cen ma bardzo duży wpływ na wiek wycofania komputera z eksploatacji.
Oszacowanie cyklu życia pozostałych elementów infrastruktury teleinformatycznej
Identyczną metodę, w celu wyznaczenia czasu wycofania urządzenia z eksploatacji, należy zastosować do pozostałych klas wyposażenia komputerowego, wykorzystując stosowne wartości dla odpowiednich współczynników poszczególnych klas wyposażenia komputerowego, które to wartości pokazano w opracowaniu Karla Whelana.
Poniżej przedstawiono zestawienie klas elementów IT z wykazem wartości poszczególnych współczynników jakich użyto, natomiast na Rysunek 8. pokazano graficzne rozwiązanie równania czasu wycofania urządzenia z eksploatacji dla poszczególnych kategorii wyposażenia komputerowego.
Tabela 2. Współczynniki modelu zużycia ekonomicznego dla poszczególnych klas elementów IT
|
Kategoria urządzeń
|
γ-g
|
s
|
δ
|
|
Komputery mainframe
|
0,25
|
0,10
|
0,01
|
|
Stacje robocze
|
0,33
|
0,25
|
0,05
|
|
Urządzenia sieciowe i telekomunikacyjne
|
0,20
|
0,18
|
0,01
|
|
Pamięci masowe
|
0,28
|
0,25
|
0,06
|
|
Drukarki
|
0,35
|
0,25
|
0,35
|
W powyższej tabeli zastosowano współczynnik r, związany ze stopą procentową obligacji rocznych skarbu państwa, równy 10%. Współczynnik ten oszacowano jako średnią od roku 1998.
Współczynnik δ, związany ze zużyciem fizycznym poszczególnych elementów infrastruktury, został w części określony według opracowania Karla Whelana , a w części oszacowany na podstawie najlepszych praktyk.
Podobnie rzecz się ma ze współczynnikiem γ – g związanym ze spadkiem cen urządzeń IT będących na podobnym poziomie rozwoju linii produktów (ang. vintage). Wszystkie współczynniki oszacowano biorąc pod uwagę wartości stosownych wskaźników ekonomicznych dla Polski w latach 1998-2004 (wzrost gospodarczy, inflacja). Warto zauważyć, że wartości zaprezentowane wcześniej (Tabela 1) odnoszą się do badań nad wyposażeniem komputerowym wyprodukowanym, co najwyżej w latach osiemdziesiątych bez uwzględnienia technologicznego zużycia. Obecnie można odnotować znacznie szybszy rozwój technologiczny aniżeli w latach osiemdziesiątych, stąd poprawki na odpowiednie wartości zużycia ekonomicznego elementów infrastruktury teleinformatycznej wyprodukowanych pod koniec lat dziewięćdziesiątych i w pierwszych latach obecnego stulecia.
Szybszy rozwój technologii teleinformatycznych w dzisiejszych czasach ma również duży wpływ na koszty związane z serwisem wyposażenia komputerowego. Stąd też współczynnik s związany z kosztem serwisu poszczególnych elementów infrastruktury został oszacowany na podstawie najlepszych praktyk.
Poniżej przedstawiono graficzne rozwiązanie równania czasu wycofania z eksploatacji dla wyodrębnionych w niniejszym opracowaniu klas infrastruktury teleinformatycznej w funkcji opłacalności eksploatacji (różnica krańcowej produktywności i kosztu serwisu).
Wiek wycofania z eksploatacji danej klasy ITS odczytuje się według punktu przecięcia osi rzędnych z krzywą reprezentującą daną klasę urządzeń (punkt, w którym krańcowa produktywność spada poniżej kosztu serwisu).
Podsumowanie i wnioski
Metoda wyznaczania cyklu życia poszczególnych klas IT podana przez Karla Whelana, dotyczy firm biznesowych, które mogą wyznaczyć realne korzyści związane z zakupem (i wycofanie z eksploatacji) wyposażenia komputerowego. Wzór ten został oparty na danych statystycznych obejmujących lata 1970-1990, a więc być może nie uwzględnia wszystkich aspektów rozwoju technologii informatycznych. Stąd też przy wyznaczaniu cyklu życia należy posługiwać się metodą najlepszych praktyk przy ustalaniu stosownych współczynników z wzoru Karla Whelana.
Dla administracji rządowej oraz firm typu non-profit (jednoosobowych firm osób fizycznych) trudno określić jaki efekt finansowy przyniosłoby firmie zastąpienie wyeksploatowanego sprzętu nowymi produktami. Ciekawą metodą (acz kosztowną i pracochłonną) byłoby wyznaczenie krańcowej produktywności i porównanie jej z kosztami serwisowania IT. Metoda ta wymagałaby rzetelnych danych z firm handlowych i producentów wyposażenia komputerowego w zakresie ustalania rzeczywistych cen ich produktów oraz stosunku tych cen do kosztów serwisowania. Nie da się ukryć, że takie dane nie są dostępne ze względu na tajemnicę handlową firm i producentów.
Jednakże należy stwierdzić, że dla administracji rządowej jak i instytucji non-profit integracja z całą gospodarką sięga tak głęboko, iż większość aspektów z zakresu infrastruktury teleinformatycznej dotyczących firm komercyjnych musi mieć swoje odbicie również przy informatyzacji administracji rządowej oraz firm typu non-profit. Rozwój technologii teleinformatycznej na rynku komercyjnym wymusza i intensyfikuje stosowne procesy w pozostałych sektorach gospodarki narodowej.
|